I first encountered a diagram of algebraic structures at the end of Jeevanjee’s second chapter, “Vector Spaces”, which elegantly summarizes the high-level differences in structure between sets, vector spaces, and inner product spaces. ¹

This diagram was immensely helpful to me, in that it helped show the relationships between various commonly used objects in mathematical physics. As I’ve encountered new structures, I’ve attempted to augment this map along two dimensions: a structure dimension that aims to measure the number of attributes an algebraic object has, and a specificity dimension which measures the amount of constraints placed on each attribute.

For instance, a Magma has more structure than a set, because a new attribute - a binary operator - has been added. A group, though, is roughly similar in structure to a magma, but has more properties of the binary operator specified, such as associativity, inverses, and identity, which make it more specific (and the magma more general). ²

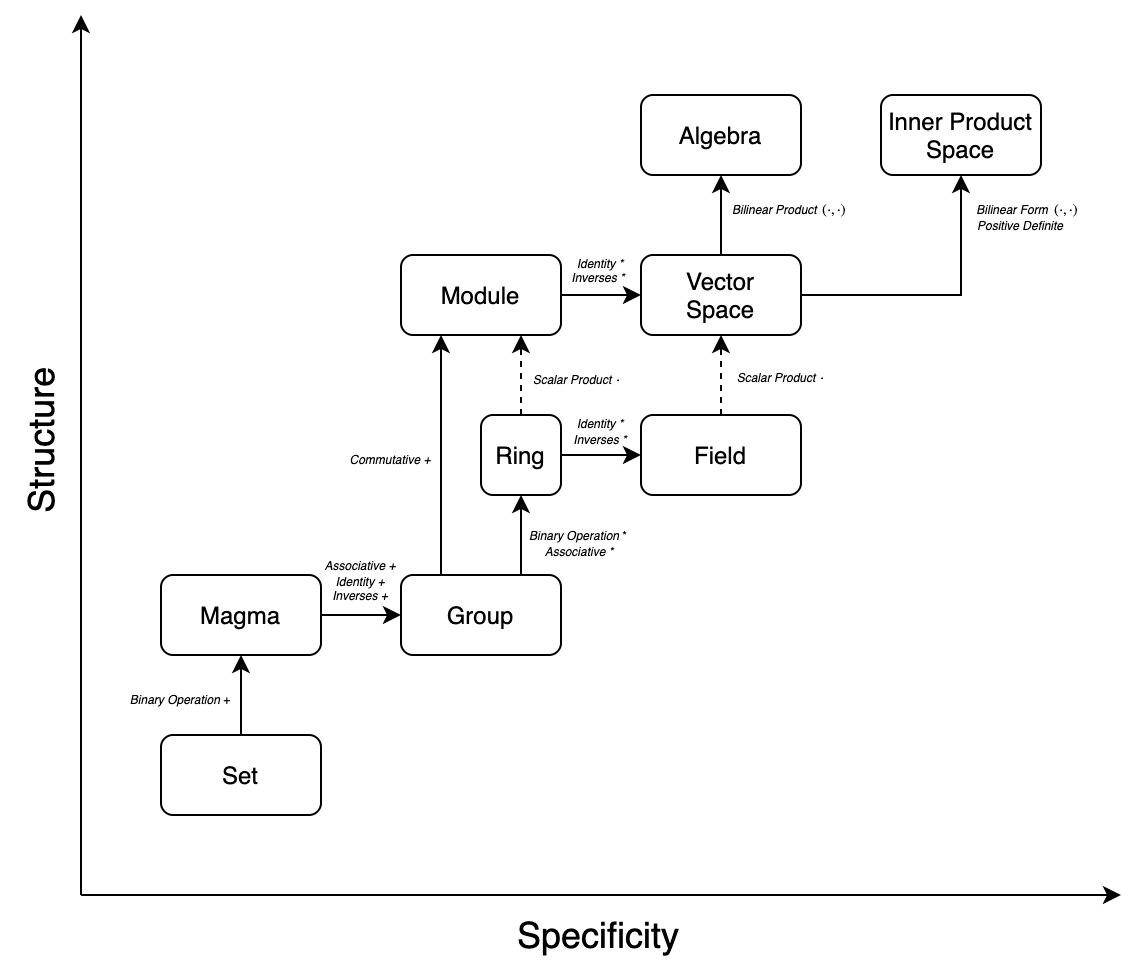
The diagram above aims to show how an algebra is constructed from a set, though admittedly omits several algebraic structures along the way. I’ve attempted to include the most primary objects used or seen in mathematical physics. I should also note, this diagram is intended as a quick-reference, and isn’t a substitute for opening Hungerford! ³